Introduction

Cancer is one of the greatest killers in the world, although medical activity has been successful, despite great difficulties, at least for some pathology. Currently the hardest challenges in modeling tumor growth and treatment are estimating parameters in models that are mathematically simple and are broadly applicable (Weinberg, 2007). The chemotherapy used in anticancer therapy for decades has significant adverse side effects. The optimization of the dosing and delivery schedule can potentially minimize adverse effects while maintaining efficacy (Frank, 2007).

Small parameter in prostate cancer diseases

We propose a mathematical model with application in prostate cancer diseases (Jackson,2004a).  Let  be the subpopulation for cancer cells in state  () at time.

Then the ordinary differential equations for no-treatment periods are given as:

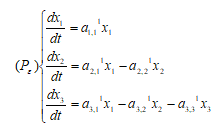
where parameters ,, represent the growth rates of populations for state 1,2,3 under the treatment condition, ,, represent the rates of influx from state 1, 1, 2 to state 2, 3, 3 under the treatment condition. Since the paths from 1 and 2 to 3 are irreversible (irreversible changes in prostate malignancy may include somatic mutations), they may be regarded as mutation rates.

 Using the program Matlab and numerical method Runge-Kutta, I did various simulations for different values of biological parameters presented in the model studied. The parameter values have highs impact on the accuracy of the model in representing real biological systems but these values are difficult to estimate experimentally. The parameters of the model are fitted to clinical data. Based on the parameters obtained from the fitting, we can predict whether the cancer will relapse or not (Jackson, 2004 b). 

Small parameter in tumors growth

We propose a mathematical model with application in tumor growth with an immune response and chemotherapy (Bru´, 2003). Mathematical models contain three variables, which are functions of time t:  the number of immune cells, the number of tumor cells,  the number of normal, or host, cells. The model is based on a set of ordinary differential system with form:

where the tumor cells as well as the normal cells are modeled by a logistic growth law, with parameters  and  representing the per capita growth rates and reciprocal carrying capacities of the two types of cells. The cells will die off at a per capita rate, and  are positive constants. The source of the immune cells is considered to be outside of the system so it is reasonable to assume a constant influx rate.

 The system of differential equations needs to be solved numerically. We used the software Matlab where we simulated the behavior of our proposed model. A baseline range of values for all eleven parameters can be determined from empirical data already in literature. The parameter set we are working with is in a region (Balkwill and Mantovani,2001).

Small parameter in two populations growth

 We assume the cancer mass to be composed by different groups of cells, distinguished genetically. To describe the tumor, we denote by  and by the two populations. Assuming that the two populations are independent of each other, the system becomes:

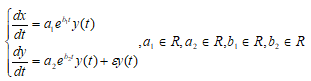
where  is a small parameter ( Venturino and  Petrovskii,2005) .

 One the equations system includes small parameter  .The smallness of   is relative to the size of the solution domain. If we reduce the size of the solution region the same small  will result in a different condition number. It is clear that the solution for a smaller region is less difficult. Using the program Matlab, we observe that in the early stage   because  is expanding and the second population is a minor clone. If  is instead the primary tumor and  is a metastasis, then because in the new site the cancer cells can freely proliferate.  Different interactions were studied, corresponding to different clinical scenarios. The growth of both populations constrained by a fixed total carrying capacity, the response to treatments, and the occurrence of spontaneous mutation and of mutations elicited by therapeutic interventions (Swan, 1990).

Small parameter in pharmacokinetic–pharmacodynamics systems

The proposed compartment model, commonly called the effect compartment in pharmacokinetic–pharmacodynamics modeling.

where  denote the concentration of the drug in plasma,denote active concentrations ,  represents the volume of distribution of the compartment,   represents the second compartment with a volume of distribution  represents the input function expressing the administration protocol,  expresses the link process between the plasma compartment where the drug is introduced,  denotes elimination ways from the plasma compartment other than ,  characterizes the  process of drug elimination from the effect compartment, where  is a small parameter (Ratain et al,1990).

 Using the program Matlab, we observe that optimal drug regimens better reduce tumors than do the protocols used in clinical practice. This new mathematical model with small parameter has been shown to be more efficient than the former ones in experimental and clinical situations. During the first phase of treatment, the number of tumor cells decreases faster than in the second phase (Wheldon 1988).

Conclusion.  An ordinary differential equations model such as the one proposed here is an essential component of a rational strategy for determining the optimal dose and schedule of chemotherapy administration. Mathematical models need to be developed to better understand how to implement this work and perhaps to elaborate new optimal treatment strategies.            The complexity of this molecular process is revealed every time a mathematical simulation of the processes is carried out. Should mention this ordinary differential model must be validated in future theoretical results and its utility will have to be confirmed in a prospective clinical trial. Interpret these results to be a permanent collaboration between mathematicians and medical oncologists. Mathematical models of tumor growth and treatment based on one or two ordinary differential equations are heavily used in practice because they are simple but can often still capture the essence of complicated interactions. The ordinary differential equations model presented here could be a useful starting point for simulating different treatment scenarios and, provided a careful validation of the parameter values is carried on extensive clinical database